Dynamic Games

#economics #micro

Oh, Hyunzi. (email: wisdom302@naver.com)
Korea University, Graduate School of Economics.
2024 Spring, instructed by prof. Cho, Wonki.

Extensive Form Game

Here, we look into dynamic game, which involves the sequential characteristics in the game:
Definition 9 (simultaneous and sequential game).

A game is simultaneous game if every player moves simultaneously, only once. And a game if sequential game if the player moves sequentially, i.e. some moves first, and other move later on.

To represent the sequential characteristics, we use the extensive form:
Definition 10 (normal and extensive form representation).

A normal (or strategic) form specifies the each player 's set of strategies and a payoff function in a matrix form.
An extensive form highlights the sequential effect and the information inside of the game. Extensive forms are represented in a game tree form, starting with an unique root, and

Here, we formally define the extensive form game.

Definition (extensive form Game).

The extensive form game is a collection where

  • : a (finite) set of nodes, .
  • : a (finite) set of actions, .
  • : a (finite) set of players, .
  • : a function specifying the single immediate predecessor of each node .
    • : only if is an initial node. otherwise, .
    • : immediate successor nodes of .
    • : set of terminal nodes.
    • : set of decision nodes, nodes except of terminal nodes.
  • :a function specifying the action for each .
    • if and , then : different nodes coming from the same predecessor must have different actions.
    • : set of choices available at decision node .
  • : a collection of information sets, .
  • : a function assigning each decision node to an information set .
    • form a partition of .
    • if : all decision nodes assigned to a single information set have the same choices available.
    • : choices available at information set .
  • : a function assigning each information set to the player who plays at .
    • if the nature plays, then denote it as player 0.
    • : player 's information sets
  • : a function assigning each actions given nature's move to the probabilities with satisfying
  • : a collection of payoff functions, where .

Bayesian Game in Extensive Form

Based on the Simultaneous-Move Games > Proposition 34 (Harsanyi's approach), we can understand the Bayesian Game in terms of the sequential game, where the nature moves first and deciding the type of the players, and then the rest of the game follows.

p
(1-p)
H
T
H
T
H
T
H
T
H
T
H
T
nature
1
2
2
2
2
2
(-1, 1)
(1, -1)
(1, -1)
(-1, 1)
(-1, 1)
(1, -1)
(1, -1)
(-1, 1)

Where , and the first node of the nature is called chance node, meaning that the type is determined by the luck.

Example (battle of sexes with incomplete information).

Consider the battle of sexes game where the player 2(wife) is the loving type with the probability with the payoff matrix of

f o
F (3, 1) (0, 0)
O (0, 0) (1, 3)

and for the probability of , the wife is leaving type with the payoff matrix of

f o
F (3, 0) (0, 3)
O (0, 1) (1, 0)

represent this Bayesian game as a extensive form game.

Proof.Note that after the first determination of the type of wife by the nature, the player 1 does not know the player 2's type. Therefore, we can re-represent the game as

love
leave
F
O
F
O
F
O
F
O
F
O
F
O
(1)
(2)
(2)
nature
(3, 1)
(0, 0)
(0, 0)
(1, 3)
(3, 0)
(0, 3)
(0, 1)
(1, 0)

Or, equivalently,

love
leave
F
O
F
O
F
O
F
O
F
O
F
O
(1)
(1)
(1)
nature
2
2
(3, 1)
(0, 0)
(0, 0)
(1, 3)
(3, 0)
(0, 3)
(0, 1)
(1, 0)

This completes the proof. □

Subgame Perfect Nash Equilibrium

Sequential Rationality

Definition (strategy).

A player's strategy is a complete, conditional plan of action.

Definition (principle of sequential rationality).

A player's strategy should specify optimal actions at every point in the game tree.

Example (predation game).
Out
In
Fight
Accommodate
E
(0, 2)
I
(-3, -1)
(2, 1)

We have two companies firm E (entrant) and firm I (incumbent). If firm E choose to go In, then the firm I can either accommodate the entrant, or fight against.

Proof.First, we specify the strategies for each players: Now we can re-represent the game into normal form game:

F if In A if In
O (0, 2) (0, 2)
I (-3, -1) (2, 1)

Here, pure strategy Nash Equilibrium are .
However, is a noncredible(empty) threat, since if the firm E chooses I, then the rational choice for the firm I will be A, not F.
Therefore, the only sequentially rational NE is . □

Backward Induction

Proposition (backward induction).

Assume a finite game of perfect information . then,

  1. Solve the optimal behavior at the end of the game (post-entry decision node). If a player is indifferent, then choose any of her optimal actions.
  2. Determine what optimal behavior is earlier in the game given the anticipation of this later behavior, and keep going.

Here, the player who moves at each decision node has a finite number of possible choices, thus optimal actions necessarily exist at each stage of the procedure.

The formal instruction for the backward induction will be discussed in Proposition 15 (generalized backward induction).

Example (3 players perfect game).
L
R
l
r
a
b
l
r
l
r
p1
p2
p3
p3
p3
(2, 0, 1)
(-1, 5, 6)
(3, 1, 2)
(5, 4, 4)
(0, -1, 7)
(-2, 2, 0)

Consider the three-player finite game of perfect information. Derive the sequentially rational Nash equilibrium using the backward induction.

Proof.First, we divide the original game into subgames:

Subgame 4
Subgame 3
Subgame 1
Subgame 2
L
R
l
r
a
b
l
r
l
r
p1
p2
p3
p3
p3
(0, -1, 7)
(-2, 2, 0)
(3, 1, 2)
(5, 4, 4)
(2, 0, 1)
(-1, 5, 6)

From Subgame 1, the optimal play of player 3 is choosing .
From Subgame 2, the optimal play of player 3 is choosing .
From Subgame 3, the optimal play of player 3 is choosing .

Thus, first reduced game is

Subgame 4
L
R
a
b
p1
p2
(5, 4, 4)
(0, -2, 7)
(-1, 5, 6)

Similarly, from Subgame 4, the optimal play of player 2 is choosing . Then, the second reduced game is

L
R
p1
(-1, 5, 6)
(5, 4, 4)

where the player 1's optimal play is choosing .

Then, the sequentially rational NE is , where the player 3's strategy is Note that there are other pure strategy Nash equilibria, but not sequentially rational. □

Proposition (Zermelo's theorem).

Every finite game of perfect information has a pure strategy Nash equilibrium that can be derived through backward induction. Moreover, if no player has the same payoffs at any two terminal nodes, then there is a unique Nash equilibrium that can be derived in this manner.

Remark that the inverse of the Proposition 8 (Zermelo's theorem) does not hold. i.e., even if there exists a unique NE derived in the game, the player can have the same payoffs in multiple terminal nodes.

Subgame Perfect Nash Equilibrium

Definition (subgame).

A subgame of an extensive form game is a subset of the game having the following properties:

  1. it begins with an information set containing a single decision node.
  2. it contains all the decision nodes that are successors (both immediate and later) of this node, and contains only these nodes.
  3. if decision node is in the subgame, then every is also in the subgame, where is the information set that contains decision node . i.e., there are no broken information sets.
Definition (subgame perfect Nash equilibrium).

A profile of strategies in an extensive form game is a subgame perfect Nash Equilibrium (SPNE) if it induces a Nash equilibrium in every subgame of .

Proposition (properties of SBNE).

Consider a game in extensive form. Then we have

  1. If the only subgame is the game as a whole, then every Nash equilibrium is subgame perfect.
  2. A subgame perfect Nash equilibrium induces a subgame perfect Nash equilibrium in every subgame of .
Example (predation game with imperfect information).
post-entry subgame
O
I
F
A
F
A
F
A
I
E
E
(0, 2)
(-3, -1)
(1, -2)
(-2, -1)
(3, 1)

From the previous example Example 5 (predation game), find the SPNE.

Proof.For the post-entry subgame, we can re-represent in a simultaneous move game.

A F
A (3, 1) (-2, -1)
F (1, -2) (-3, -1)

In the post-entry subgame, the only pure strategy NE is . Then the reduced game is

O
I
E
(3, 1)
(0, 2)

Considering this, the SPNE is which is the unique equilibrium. □

Example (centipede game).
C
C
C
C
C
S
S
S
S
S
S
S
(1, 1)
(0, 3)
(2, 2)
(97, 100)
(99, 99)
(98, 101)
(100, 100)
1
1
1
1
1
1

In the finite game of perfect information, two players 1 and 2 start with 1 dollar in front of game. Starting with player 1, each player can either continue (C) or stop (S). Using the backward induction, the only SPNE is resulting in the payoff .

Existence of Subgame Perfect Nash Equilirbium

Proposition (existence of pure SPNE).

Every finite game of perfect information has a pure strategy subgame perfect Nash equilibrium (SPNE). Moreover, if no player has the same payoffs at any two terminal nodes, then there is a unique subgame perfect Nash equilibrium.

Proposition (generalized backward induction).
  1. Start at the enc of the game tree, and identify the Nash equilibria for each of the final subgames (i.e., those that have no other subgames nested within them).
  2. Select one Nash equilibrium in each of these final subgames.
  3. Derive the reduced extensive form game in which the final subgames in step 2 are replaced by the payoffs that result in these subgames when players use these equilibrium strategies.
  4. Repeat steps 1 to 3 for the reduced game. Continue the procedure until every move in is determined. The resulting collection of moves at the various information sets of constitutes a profile of SPNE strategies.

If multiple equilibria are never encountered in any step of this process, then the strategy profile is the unique SPNE. If multiple equilibria are encountered, the full set of SPNEs is identified by repeating the procedure for each possible equilibrium that could occur for the subgames in question.

Here we briefly introduce how the generalized backward induction procedure can identify the set of SPNEs.

Proposition (SPNE resulting from genealized backward induction).

Consider an extensive form game and some subgame of .
Suppose that strategy profile is an SPNE in subgame , and let be the reduced game formed by replacing subgames by a terminal node with payoffs equal to those arising from play of . Then:

  1. In any SPNE of in which is the play in subgame , players' moves at information sets outside subgame must constitute an SPNE of reduced game .
  2. If is an SPNE of , then the strategy profile that specifies the moves in at information sets in subgame and that specifies the moves in at information sets not in is an SPNE of .
Example (Niche Choice game with imperfect information).

Consider a modification of Example 12 (predation game with imperfect information), in which there are two niches in the market, one large and one small, and two firms decide simultaneously which niche they will be in.

post-entry subgame
O
I
S
L
S
L
S
L
I
E
E
(0, 2)
(-6, -6)
(-1, 1)
(1, -1)
(-3, -3)

Find the SPNE.

Proof.For the post-entry subgame, we can re-represent in a simultaneous move game.

S N
S (-6, -6) (-1, 1)
N (1, -1) (-3, -3)

Then the pure Nash equilibium of this post-entry subgame is and .

When the subgame NE is , the reduced form game is

O
I
E
(1, -1)
(0, 2)

Therefore, the SPNE is .

When the subgame NE is , the reduced form game is

O
I
E
(-1, 1)
(0, 2)

Thus the SPNE is . □

Perfect Bayesian Equilibrium

Weak Perfect Bayesian Equilibrium

Definition (system of beliefs).

A system of beliefs in extensive form game is a specification of a probability for each decision node such that

Definition (expected payoff starting at information set).

Player 's expected payoff starting at her information set is where her beliefs regarding the conditional probabilities of being at the various nodes in are given by , and the strategy is being played.

Definition (sequentially rational).

A strategy profile in extensive form game is sequentially rational at information set given a system of beliefs , if where is the player who moves at information set .
Moreover, if the strategy profile is sequentially rational at all information set given , i.e. then we say that is sequentially rational given belief system .

Remark (bayes' rule).

For each node in a given player's information set , the player should compute the probability of reaching that node, given play of strategies : Using this probability, the player should assign conditional probabilities of being at each of these nodes given that play has reached this information set: which is based on the Bayes' rule.

Definition (weak perfect bayesian equilibrium).

A profile of strategies and system of beliefs is a weak perfect Bayesian Equilibrium (WPBE) in extensive form game if it has following properties:

  1. The strategy profile is sequentially rational given belief system .
  2. The system of beliefs is derived from strategy profile through Bayes' rule whenever possible:
    • For every information set with , the beliefs is
    • For the information set with , can have arbitrary value for .

WPBE in Discrete Type Space

Example (predation game of WPBE).
H
O
I1
I2
F
A
F
A
I
E
[μ]
[1-μ]
(0, 2)
(-1, -1)
(3, 0)
(-1, -1)
(2, 1)

From the previous example Example 5 (predation game), find the WPBE.

Proof.Let denote the probability that firm assigns to being at the left hand node in her information set . We first determine the value of that supports firm 's choice of over .: since for all , firm always chooses .

Given this information, firm now choose between the three:

O
I1
I2
E
(3, 0)
(2, 1)
(0, 2)

where choosing is rational for the firm .

Now, as firm 's belief must satisfy the bayes' rule:

Thus, the pair of is the unique WPBE in this game (pure or mixed). □

Example (predation game of WPBE 2).
H
O
I1
I2
F
A
F
A
I
E
[μ]
[1-μ]
(0, 2)
(-1, 1)
(1, 2)
(2, 0)
(-2, -1)

From the previous example Example 5 (predation game), find the WPBE.

Proof.Let denote the probability that firm assigns to being at the left hand node in her information set . We first determine the value of that supports firm 's choice of over .: Thus, firm 's choice follows where denotes the probability that the firm plays at the information set .

case 1) If , the firm always chooses . Thus, firm chooses . Therefore, .

case 2) If , the firm always chooses . Thus, firm chooses . Therefore, .

case 3) If , firm 's expected payoff is thus we have where denotes the probability that firm plays . Note that at , firm is indifferent among all .

Note that if , the result will be equal to the case 2, and if , the result will be equal to the case 1. Therefore the only remaining case is when .

Using bayes' rule, Thus, for any , where and can be the solution.

Therefore, the WPBE is where and . □

Example (joint venture entry game).
I
Out
EO
PJV
Accept
Decline
In
Out
F
A
F
A
F
A
(0, 0, 3)
(-1, 0, 2)
(2, 0, 1)
(1, 1, -2)
(4, 4, 0)
(-1, 0, 2)
(2, 0, 1)
E1
E2
E1
(0, 0, 3)

Where means "Enter on Own", and means "Propose Joint Venture". Find the WPBE.

Proof.follow the logic below:

  1. For E2, since
    • if Accommodate, then the payoff of E2 is either of .
    • if Decline, then the payoff of E2 is always 0.
    • thus is strictly preferred than .
  2. For E1, is strictly dominating
    • If I always plays , then E1 plays
      • if E1 plays , then the payoff is 0.
      • if E1 plays , then the payoff is -1.
      • if E1 plays , then the payoff is 1 (given E2 plays from 1).
    • If I always plays , then E1 plays
      • if E1 plays , then the payoff is 0.
      • if E1 plays , then the payoff is 2.
      • if E1 plays , then the payoff is 4 (given E2 plays from 1).
    • thus is strictly dominating than others.
  3. Given strategies of E1 and E2, middle note of the information set is sure to be located, thus
  4. Given , I will always chooses .
  5. Then, at the node of E1 following E2's decline, E1 plays .

Therefore, we have which completes the proof. □

Sequential Equilibrium

The Definition 22 (weak perfect bayesian equilibrium) has one big drawback, which is a result from the second condition, that does not define the condition of the system of belief on the information set that has no probability to be reached under given . This is because from when , then cannot be defined as the denominator is zero.

Definition (sequential equilibrium).

A strategy profile and system of beliefs is a sequential equilibrium of extensive form game if it has the following properties:

  1. strategy profile is sequentially rational given belief system .
  2. there exists a sequence of completely mixed strategies , with where denotes the beliefs derived from strategy profile using Bayes' rule:
Example (two players two information set).

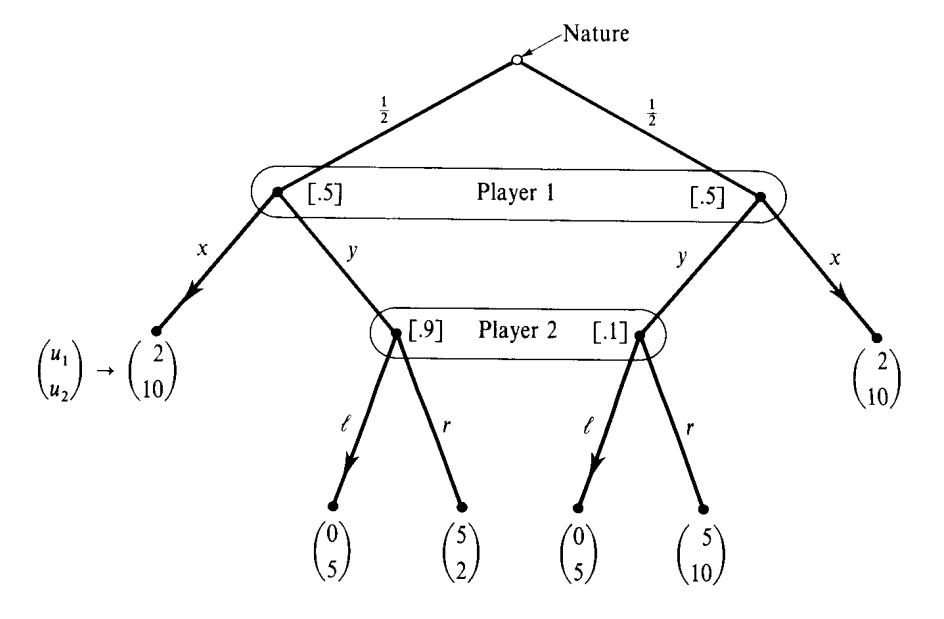
Pasted image 20240611132132.png
Where we denote the information set of player 1 as and the information set of player 2 as . And denote be the probability that the player 1 is located at left node at , (i.e. ), and .

Proof.Before solving the problem, remark that in , as the nature's choice for the left and the right node is equally given as , it is rational to have First, assume that the player 2 arrived in . Then, Thus, the response of the player 2 is where denotes the probability that the player 2 chooses at .

case 1) if , then player 2 chooses always. Thus, the expected payoff of player 1 is thus for player 2, we have .
Then, we have , meaning that any is possible for WPBE. Then,

case 2) if , then player 2 chooses always. Thus, the expected payoff for player 1 is thus for player 2, we have .
Then, applying the bayes' rule, we have which shows that the belief is consistent with the given strategy. Therefore,

case 3) if , then player 2 mixes her strategy. By denoting be the probability that the player 2 chooses in her mixed strategy, the expected payoff for player 1 is thus the response for player 1 is where denotes the probability of choosing at .
Note that, however, by the bayes' rule, we have for any , meaning that in any strategies for the case 3 is inconsistent with the belief.

Summing up, we have two WPBE, where Now, we narrow down WPBE to SE for the case 1. While we could not apply bayes' rule in the case 1, as the denominator was zero, consider an arbitrary sequence of where Then, we have thus it is inconsistent for any if the belief is given as . Therefore, we have as an only sequential equilibrium. □

Interactive Graph
Table Of Contents
Dynamic Games
Extensive Form Game
Bayesian Game in Extensive Form
Subgame Perfect Nash Equilibrium
Sequential Rationality
Backward Induction
Subgame Perfect Nash Equilibrium
Existence of Subgame Perfect Nash Equilirbium
Perfect Bayesian Equilibrium
Weak Perfect Bayesian Equilibrium
WPBE in Discrete Type Space
Sequential Equilibrium